Electricity Class 10 Important Questions & Answers with Numericals

Get ready for your Class 10 Science exam with these important questions and answers from Chapter 11 Electricity accompanied by numericals with their detailed solution. Everything you need for top marks is here!

Subject	Science (Physics)
Class	10
Board	CBSE
Chapter No.	11
Chapter Name	Electricity
Type	Questions and Answers
Session	2024-25

"Believe in yourself and all that you are. Know that there is something inside you that is greater than any obstacle."

- Christian D. Larson

Electricity Class 10 Important Questions and Answers with Numerical Problems

Q. No. 1) Multiple Choice Questions (MCQs)

i. A battery of 10 volts carries 20,000 C of charge through a resistance of 20 Ω. The work done in 10 seconds is _____.

a. 2 x 10² joule

b. 2 x 10⁵ joule

c. 2 x 10⁴ joule

d. 2 x 10³ joule

Ans. Option (b) [V = ^W/_Q ⇒ W = V x Q = 10 x 20000 = 200000 = 2 x 10⁵ joule]

ii. A boy records that 4000 joules of work is required to transfer 10 coulombs of charge between two points of a resistor of 50 Ω. The current passing through it is _____.

a. 2 A

b. 4 A

c. 8 A

d. 16 A

Ans. Option (c)

[V = ^W/_Q = ⁴⁰⁰⁰/₁₀ = 400

V = IR ⇒ I = ^V/_R = ⁴⁰⁰/₅₀ = 8 A]

iii. All elements of an electric circuit are connected in series except

a. Voltmeter

b. Ammeter

c. Rheostat

d. Resistor

Ans. Option (a) [Rheostat is a variable resistor. We can increase/decrease its resistance.]

iv. A resistance wire is stretched so as to double its length. Its new resistivity will have a magnitude

a. 2 times its original value

b. 4 times its original value

c. 8 times its original value

d. Same as its original

Ans. Option (d) [resistivity depends on the nature of material]

v. Study the V-I graph for four conductors A, B, C, and D having resistance R_A, R_B, R_C, and R_D respectively and which one of the following relations is true for these conductors.

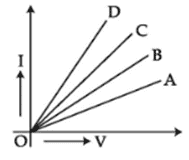
a. R_A > R_B > R_C > R_D

b. R_A < R_B < R_C < R_D

c. R_A = R_B = R_C = R_D

d. R_A = R_B < R_C < R_D

Ans. Option (a)

vi. Three V-I graphs are drawn individually for two resistors and their series combination. Out of A, B, and C which one represents the graph for a series combination of the other two?

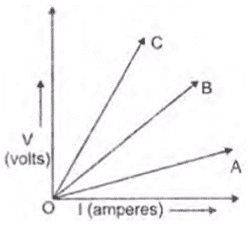
a. A

b. B

c. C

d. None of the above

Ans. Option (c) [More slope of V-I graph means more resistance. The slope of C is maximum, so its resistance is maximum.]

vii. When a 4 V battery is connected across an unknown resistor there is a current of 100 mA in the circuit. The value of the resistance of the resistor is:

a. 4 Ω

b. 40 Ω

c. 400 Ω

d. 0.4 Ω

Ans. Option (b) [V = IR ⇒ R = V/I = ⁴/_(100/1000) = 40 Ω]

viii. Plastic insulation surrounds a wire having diameter d and length l as shown below.

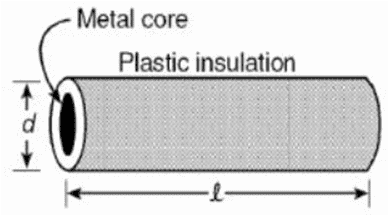
A decrease in the resistance of the wire would be produced by an increase in the:

a. Length l of the wire

b. Diameter d of the wire

c. Temperature of the wire

d. Thickness of the plastic insulation

Ans. Option (b)

ix. Raman wants to draw a graph to show how the resistivity (ρ) of a wire changes with the length (l) of the wire.

What should his graph look like?

Ans. Option (D)

x. What is the maximum resistance which can be made using five resistors each of ¹/₅ Ω?

a. ¹/₅ Ω

b. 10 Ω

c. 5 Ω

d. 1 Ω

Ans. Option (d)

xi. A piece of wire of resistance R is cut into five equal parts. These parts are then connected in parallel. If the equivalent resistance of this combination is R’, then the ratio ^R/_R’ is:

a. ¹/₂₅

b. 5

c. 10

d. 25

Ans. Option (d)

xii. The circuit below consists of a variable resistor connected in series with two 2000 Ω resistors. The variable resistor can be adjusted to any value between 0-4000 Ω.

As the resistance of the variable resistor is changed, what is the smallest possible reading on the voltmeter?

a. 0 V

b. 3 V

c. 4 V

d. 6 V

Ans. Option (b)

xiii. The resistance between A and B in the given figure will be

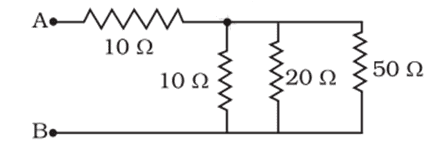
a. 20 Ω

b. 30 Ω

c. 90 Ω

d. More than 10 Ω but less than 20 Ω

Ans. Option (d)

[ ¹/_R = ¹/₁₀ + ¹/₂₀ + ¹/₅₀ = ¹⁷/₁₀₀

⇒ R= ¹⁰⁰/₁₇

Total resistance = 10 + ¹⁰⁰/₁₇ = ²⁷⁰/₁₇ = 15.88 Ω]

xiv. A complete circuit is left on for several minutes, causing the connecting copper wire to become hot. As the temperature of the wire increases, the electrical resistance of the wire

a. Decreases

b. Remains the same

c. Increases

d. Increases for some time and then decreases

Ans. Option (c)

xv. In the following given circuits, the heat produced in the resistor or combination of resistors connected to a 12 V battery will be

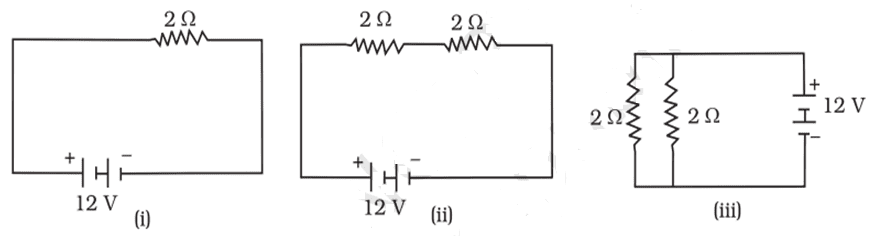
a. Same in all the cases

b. Minimum in case (i)

c. Maximum in case (ii)

d. Maximum in case (iii)

Ans. Option (d)

[Case (i): I = ^V/_R = ¹²/₂ = 6 A

H = I²Rt = 6 x 6 x 2 t = 72 t

Case (ii): R = 2 + 2 = 4 Ω

I = ^V/_R = ¹²/₄ = 3 A

H = I²Rt = 3 x 3 x 4 t = 36 t

Case (iii): R = ^{2 x 2}/ _{2 + 2} = 1 Ω

I = ^V/_R = ¹²/₁ = 12 A

H = I²Rt = 12 x 12 x 1 t = 144 t]

xvi. Two conducting wires of the same material and of equal lengths and equal diameters are first connected in series and then parallel in a circuit across the same potential difference. The ratio of heat produced in series and parallel combinations would be:

a. 1:2

b. 2:1

c. 4:1

d. 1:4

Ans. Option (d)

xvii. Assertion: A fuse wire is always connected in parallel with the mainline.

Reason: If a current larger than the specified value flows through the circuit, the fuse wire melts.

Options

a. Both A and R are true and R is the correct explanation of A

b. Both A and R are true but R is not the correct explanation of A

c. A is true but R is false

d. A is false but R is true

Ans. Option (d)

xviii. In an electrical circuit three incandescent bulbs A, B, and C of rating 40 W, 60 W, and 100 W are connected in parallel to an electric source. Which of the following is likely to happen regarding their brightness?

a. Brightness of all the bulbs will be the same

b. The brightness of bulb A will be the maximum

c. The brightness of bulb B will be more than that of A

d. The brightness of bulb C will be less than that of B

Ans. Option (c) [In a parallel connection, the bulb with the highest power glows the brightest]

xix. Unit of electric power may also be expressed as:

a. volt-ampere

b. kilowatt-hour

c. watt-second

d. joule-second

Ans. Option (a)

xx. An electric bulb is rated 220 V and 100 W. When it is operated on 110 V, the power consumed will be:

a. 100 W

b. 75 W

c. 50 W

d. 25 W

Ans. Option (d)

[R = V²/P = ^{220 x 220}/₁₀₀ = 484 Ω

V’ = 110 V

∴ P = V²/R = ^{110 x 110}/₄₈₄ = 25 W]

xxi. Match the following

Column I	Column II
A. Ohm	I. ρL/A
B. Resistance	II. 1 volt/1 ampere
C. Resistivity	III. zero resistance
D. Superconductor	IV. ohm-meter

Ans. A-II, B-I, C-IV, D-III

xxii. Column A contains some electrical devices and Column B contains the material used for making these devices. Match Columns A and B.

Column A	Column B
1. Filament of electrical bulb	A. Copper
2. Heating elements	B. Lead-tin alloy
3. Connection wire	C. Tungsten
4. Fuse wire	D. Nichrome

Ans. 1-C, 2-D, 3-A, 4-B

Q. No. 2) If the charge on an electron is 1.6 x 10^-19 C, find the approximate number of electrons in 1 C.

Ans. 1.6 x 10^-19 C charge contains = 1 electron

⇒ 1 C charge contains = 1/1.6 x 10^-19 electrons = 6.25 x 10¹⁸ electrons.

Q. No. 3) Calculate the number of electrons that would flow per second through the cross-section of a wire when 1 A current flows in it.

Ans. I = 1 A, t = 1 s

∴ I = ^Q/_t

⇒ Q = It = 1 x 1 = 1 C

⇒ ne = 1

⇒ n = ¹/_e = 1/1.6 x 10^-19 = 6.25 x 10¹⁸ electrons

Q. No. 4) Calculate the amount of charge flowing in a wire if it draws a current of 2 mA in 10 seconds.

Ans. Q = It = 2 x 10^-3 x 10 = 0.02 C

Q. No. 5) i. When do we say that the potential difference between two points of a circuit is 1 volt?

ii. Some work is done to move a charge Q from infinity to point A in space. The potential of point A is given as V. What is the work done to move this charge from infinity in terms of Q and V?

Ans. i. The potential difference between two points of an electric circuit is said to be 1 volt when a work of 1 J is to be done for moving a charge of 1 C between two points.

ii. W = QV

Q. No. 6) List the differences between a voltmeter and an ammeter.

Ans.

Voltmeter	Ammeter
i. It is used to measure the potential difference across two points in an electric circuit.	i. It is used to measure electric current in an electric circuit.
ii. Its resistance is very high.	ii. Its resistance is very low.
iii. It is connected in parallel in an electric circuit.	iii. It is connected in series in an electric circuit.

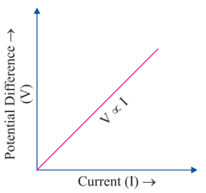
Q. No. 7) State Ohm’s Law.

Ans. Ohm’s Law: Potential difference across the two points of a metallic conductor is directly proportional to the current passing through the circuit provided that temperature remains constant.

Mathematical expression of Ohm’s Law:

V ∝ I

⇒ V = IR

R is a constant called resistance for a given metal.

V-I graph for Ohm’s Law:

Q. No. 8) The values of current I flowing in a given resistor for the corresponding values of potential difference V across the resistor are given below:

I (ampere)	V (volt)
0.5	1.6
1.0	3.4
2.0	6.7
3.0	10.2
4.0	13.2

Plot a graph between V and I and calculate the resistance of the resistor.

Ans.

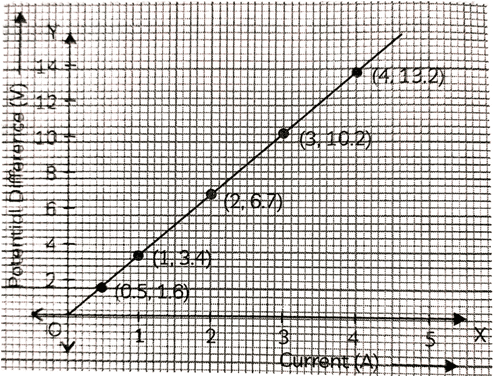
R = Slope of graph = ^ΔV/_ΔI = ^{13.2 - 1.6}/_4.0-1.0 = ^11.6/_3.0  = 3.86 Ω

Q. No. 9) Study the V-I graph for a resistor as shown in the figure and prepare a table showing the values of I (in amperes) corresponding to four different values of V (in volts). Find the value of current for V = 10 volts. How can we determine the resistance of the resistor from this graph?

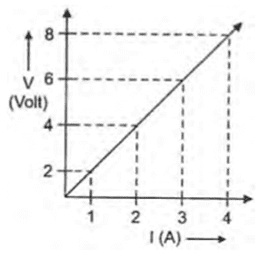
Ans.

V (volt)	I (ampere)
2	1
4	2
6	3
8	4

R = Slope of graph = ^ΔV/_ΔI = ^8-2/_4-1 = ⁶/₃  = 2 Ω.

Q. No. 10) List the factors on which the resistance of a wire depends.

Ans. Resistance of a uniform metallic conductor is:

1. Directly proportional to the length of the conductor (l).
2. Inversely proportional to the area of cross-section (A).
3. Directly proportional to the temperature.
4. Depend on the nature of the material (ρ).

R = ^ρl/_A

Q. No. 11) A wire of resistance 5 Ω is bent in the form of a closed circle. Find the resistance across the diameter of the circle.

Ans.

R = 5 Ω

∴ Resistance of semicircle = 5/2 Ω

Both the semicircle are in parallel connection.

¹/_Req = ¹/_5/2 + ¹/_5/2 = ²/₅ + ²/₅ = ⁴/₅ Ω

⇒ R_eq = ⁵/₄ Ω

Q. No. 12) Six equal resistance of 1 Ω are connected to form a hexagon ABCDEFA. Estimate the resistance offered by combination if the current enters at one point and leaves at the opposite end.

Ans.

Resistance of ABCD = R₁ = 1 + 1 + 1 = 3 Ω

Resistance of AFED = R₂ = 1 + 1 + 1 = 3 Ω

Now, ABCD and AFED are in parallel combination.

The resistance between A and D

¹/_R = ¹/_R1 + ¹/_R2 = ¹/₃ + ¹/₃ = ²/₃

⇒ R = ³/₂ Ω = 1.5 Ω

Q. No. 13) A student boils water in an electric kettle for 20 minutes. Using the same mains supply he wants to reduce the boiling time of water. To do so should he increase or decrease the length of the heating element? Justify your answer.

Ans. To reduce the boiling time using the same mains supply, the rate of heat (power) production should be large.

We know, P = V²/R

Since V is constant, R should be decreased. Since R is directly proportional to length, the length should be decreased.

Q. No. 14) A 4 Ω resistance wire is doubled on it. Calculate the new resistance of the wire.

Ans. Here the length of the wire will get half and the area of the cross-section will get doubled.

Let the resistance of the wire originally be ‘R’, length ‘l’, and the area of cross-section ‘A’ with the resistivity of the material is ‘ρ’.

Therefore, R = ^ρl/_A

⇒ 4 = ^ρl/_A

Now, for the new arrangement,

Resistance = ^ρ(l/2)/_2A = (¹/₄)^ρl/_A = ¹/₄ x 4 = 1 Ω.

Q. No. 15) A wire of resistivity ρ is stretched to double its length. How does it affect the

a. resistance

b. resistivity?

Ans. a. Let the resistance of the wire originally be ‘R’, length ‘l’, and area of cross-section ‘A’.

Therefore, R = ^ρl/_A

The wire is stretched to double its length.

New length of wire l’ = 2l

New area of cross-section A’ = ^A/₂

New resistance R’ = ^{ρ x 2l}/_A/2 = 4 ^ρl/_A = 4R

b. Resistivity will remain the same as it depends on the nature of the material of the wire.

Q. No. 16) A wire of resistance 10 Ω is drawn out so that its length is thrice its original length. Solve and find the resistance of the new wire.

Ans. Let the resistance of the wire originally be ‘R’, length ‘l’, and the area of cross-section ‘A’ with the resistivity of the material is ‘ρ’.

Therefore, R = ^ρl/_A

⇒ 10 = ^ρl/_A

Now, the new length of wire = 3l

New area of cross-section = ^A/₃

New resistance R’ = ^ρ3l/_A/3 = 9 ^ρl/_A = 9 x 10 = 90 Ω

Q. No. 17) The figure below shows three cylindrical copper conductors along with their face areas and lengths.

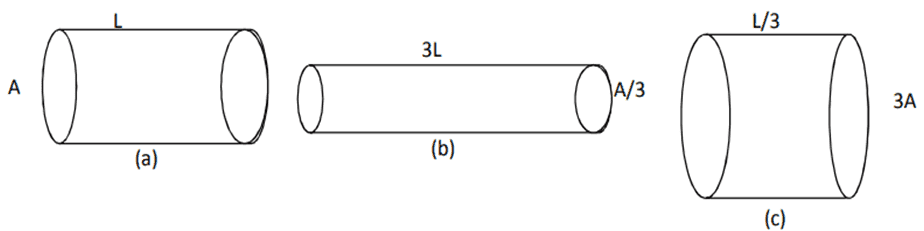
Compare the resistance and the resistivity of the three conductors. Justify your answer.

Ans.  R_a = ^ρL/_A

R_b = ^ρ3L/_A/3 = 9 ^ρL/_A

R_c = ^ρL/3/_3A = ¹/₉ ^ρL/_A

∴ R_b > R_a > R_c [Since ρ_a = ρ_b = ρ_c because all the three conductors are of the same material.]

Q. No. 18) i. Consider a conductor of resistance ‘R’, length ‘L’, thickness ‘d’, and resistivity ‘ρ’. Now, this conductor is cut into four equal parts. What will be the new resistivity of each of these parts? Why?

ii. Find the resistance if all of these parts are connected in:

a. Parallel

b. Series

iii. Out of the combination of resistors mentioned above in the previous part, for a given voltage which combination will consume more power and why?

Ans. i. Resistivity will remain the same as it depends on the nature of the material of the conductor.

ii. The length of each part = ^L/₄

Resistivity (ρ) and area of cross-section (A) will remain constant.

Initial resistance of conductor = R = ^ρL/_A

Resistance of each part = R’ = ^ρL/4/_A = ¹/₄ ^ρL/_A = ^R/₄

a. Parallel connection:

¹/_Req = ¹/_R’ + ¹/_R’ + ¹/_R’ + ¹/_R’ = ⁴/_R’ = ⁴/_R/4 = ¹⁶/_R

⇒ R_eq = ^R/₁₆ Ω

b. Series connection:

R_eq = ^R/₄ + ^R/₄ + ^R/₄ + ^R/₄ = ^4R/₄ = R Ω

iii. P = V²/R

If R_eq is less, the power consumed will be more.

In the given case, R_eq is lesser in the parallel so the power consumed will be more in parallel.

Q. No. 19) Two unequal resistances are connected in parallel. If you are not provided with any other parameters (eg. numerical values of I and R), what can be said about the voltage drop across the two resistors?

Ans. Voltage drop is the same across both.

Q. No. 20) Draw a circuit diagram of an electric circuit containing a cell, a key, an ammeter, and a resistor of 4 Ω in series with a combination of two resistors (8 Ω each) in parallel and a voltmeter across a parallel combination. Each of them dissipates maximum energy and can withstand a maximum power of 16W without melting. Find the maximum current that can flow through the three resistors.

Ans.

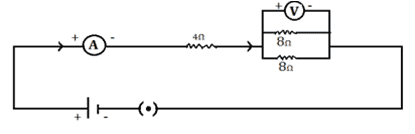
The maximum current through a 4 Ω resistor

P = I²R

⇒ I² = ^P/_R = ¹⁶/₄ = 4

⇒ I = 2 A

∴ The maximum current through each 8 Ω resistor = ²/₂ = 1 A

Q. No. 21) Three 2 Ω resistors, A, B, and C are connected as shown below. Each of them dissipates and can stand a maximum power of 18 W without melting. Find the maximum current that can flow through the three resistors.

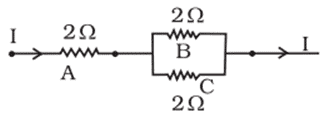
Ans. The maximum current through resistor A

P = I²R

⇒ I² = ^P/_R = ¹⁸/₂ = 9

⇒ I = 3 A

∴ The maximum current through resistors B and C each = ³/₂ = 1.5 A

Q. No. 22) Draw a circuit diagram of an electric circuit containing a cell, a key, an ammeter, and a resistor of 2 Ω in series with a combination of two resistors (4 Ω each) in parallel and a voltmeter across the parallel combination. Will the potential difference across the 2 Ω resistors be the same as that across the parallel combination of 4 Ω resistors? Give reason.

Ans.

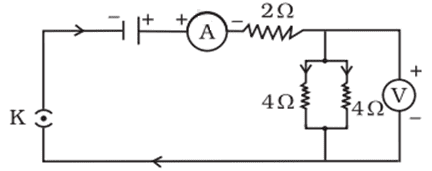
Yes, because the total resistance of the parallel combination is also 2 Ω.

Q. No. 23) In the given circuit, A, B, C, and D are four lamps connected with a battery of 60 V.

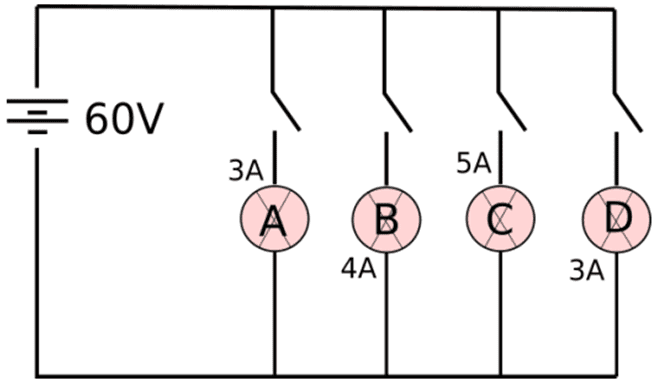
Analyze the circuit to answer the following questions.

i. What kind of combination are the lamps arranged in (series or parallel)?

ii. Explain with reference to your above answer, what are the advantages of this combination of lamps.

iii. Explain with proper calculations which lamp glows the brightest?

iv. Find out the total resistance of the circuit.

Ans. i. The lamps are in parallel connection.

ii. Advantages of parallel combination over series combination:

1. If one appliance stops working or goes out of order, then all other appliances keep on working.
2. All appliances can be operated at the same voltage as the electric supply.
3. Different appliances have different requirements of current. This cannot be satisfied in series as the current remains the same in series.
4. The total resistance in a parallel circuit is decreased.
5. All devices can be operated independently with separate switches.

iii. The lamp with the highest power will glow the brightest.

P = VI

In this case, all the bulbs have the same voltage. But lamp C has the highest current.

Hence, for lamp C, P = 5 x 60 = 300 W.

iv. Total current in the circuit = 3 + 4 + 5 + 3 = 15 A

The voltage = 60 V

Now, V = IR

⇒ R = ^V/_I = ⁶⁰/₁₅ = 4 A

Q. No. 24) The diagram above is a schematic diagram of a household circuit. The house shown in the above diagram has 5 usable spaces where electrical connections are made. For this house, the mains have a voltage of 220 V and the net current coming from the mains is 22A.

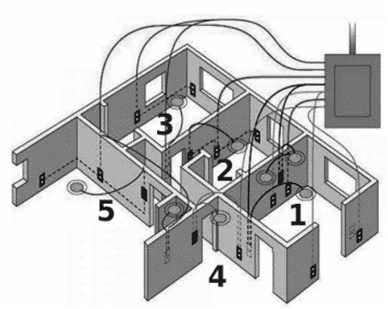
a. What is the mode of connection to all the spaces in the house from the mains?

b. Spaces 5 and 4 have the same resistance and spaces 3 and 2 have respective resistances of 20 Ω and 30 Ω. Space 1 has a resistance double that of space 5. What is the net resistance for space 5?

c. What is the current in space 3?

d. What should be placed between the main connection and the rest of the house’s electrical appliances to save them from accidental high electric current?

Ans. a. All spaces are connected in parallel.

b. Let the resistance of spaces 4 and 5 be R Ω

Resistance of Space 1 = 2R Ω

Resistance of Space 2 = 30 Ω

Resistance of Space 3 = 20 Ω

Current = 22 A

V = 220 V

Total resistance R_eq = ^V/_I = ²²⁰/₂₂ = 10 Ω

Now,

¹/_Req = ¹/_R1 + ¹/_R2 + ¹/_R3 + ¹/_R4 + ¹/_R5

⇒ ¹/₁₀ = ¹/_2R + ¹/₃₀ + ¹/₂₀ + ¹/_R + ¹/_R

⇒ ⁵/_2R = ¹/₁₀ - ¹/₃₀ + ¹/₂₀ = ¹/₆₀

⇒ R = 60 x ⁵/₂ = 150 Ω

c. I₃ = ^V/_R3 = ²²⁰/₂₀ = 11 A

d. Fuse.

Q. No. 25) In the circuit given below if the current reading in the ammeter A is 2 A, what would be the value of R₁?

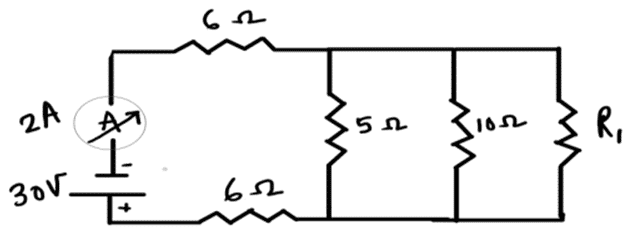
Ans. Total resistance of the circuit = R_eq = ^V/_I =³⁰/₂ = 15 Ω

5 Ω, 10 Ω, and R₁ are in parallel.

∴ ¹/_Rp = ¹/₅ + ¹/₁₀ + ¹/_R1

⇒ ¹/_Rp = ^{3R1 + 10}/_10R1

⇒ R_p = ^10R1/_{3R1 + 10}

Now, 6 Ω, R_p, and 6 Ω are in series.

∴ R_eq = 6 + 6 + ^10R1/_{3R1 + 10} = 12 + ^10R1/_{3R1 + 10}

⇒ 15 = 12 + ^10R1/_{3R1 + 10}

⇒ 3 (3R₁ + 10) = 10R₁

⇒ R₁ = 30 Ω

Q. No. 26) Calculate the total resistance of the circuit and find the total current in the circuit.

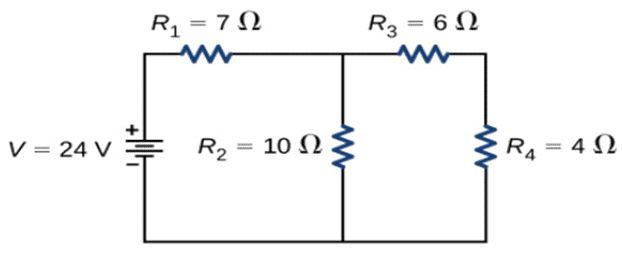
Ans. Equivalent resistance of R₃ and R₄ (in series) = R₃ + R₄ = 6 + 4 = 10 Ω = R₅

Equivalent resistance of R₂ and R₅ (in parallel) = ^{R2 x R5}/_{R2 + R5} = ^{10 x 10} /_{10 + 10} = ¹⁰⁰/₂₀ = 5 Ω = R6

Equivalent resistance of R₁ and R₆ (in series) = R₁ + R₆ = 7 + 5 = 12 Ω

Now, by Ohm’s law,

V = IR

⇒ I = ^V/_R = ²⁴/₁₂ = 2 A

Q. No. 27) A student has two resistors – 2 Ω and 3 Ω. She has to put one of them in place of R₂ as shown in the circuit. The current that she needs in the entire circuit is exactly 9 A. Show by calculation which of the two resistors she should choose.

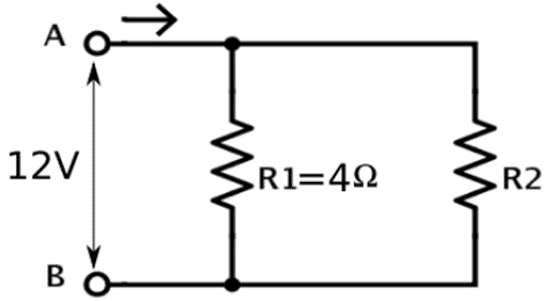
Ans. The overall current needed = 9 A. The voltage is 12 V.

∴ Total resistance R = ^V/_I = ¹²/₉ = ⁴/₃ Ω.

Now, R₁ and R₂ are in parallel.

∴ ¹/_R = ¹/_R1 + ¹/_R2

⇒ ¹/_4/3 = ¹/₄ + ¹/_R2

⇒ ¹/_R2 = ³/₄ - ¹/₄ = ²/₄ = ¹/₂

⇒ R₂ = 2 Ω

Q. No. 28) Calculate the value of each resistance which when connected in parallel gives a resultant value of 2 Ω and when connected in series the resultant value becomes 9 Ω.

Ans. Let R and r be the two resistances.

A.T.Q, R + r = 9

⇒ r = 9 – R

And, ^{R x r}/_R+r = 2

⇒ ^{R x r}/₉ = 2

⇒ R x r = 18 Ω

⇒ R x (9 – R) = 18

⇒ 9R – R² = 18

⇒ R² -9R + 18 = 0

⇒ R² -6R -3R + 18 = 0

⇒ (R – 3) (R – 6) = 0

⇒ R = 3 Ω Or 6 Ω

If R = 3 Ω, r = 9-3=6 Ω and vice versa.

Q. No. 29) In the circuit shown below, solve and calculate:

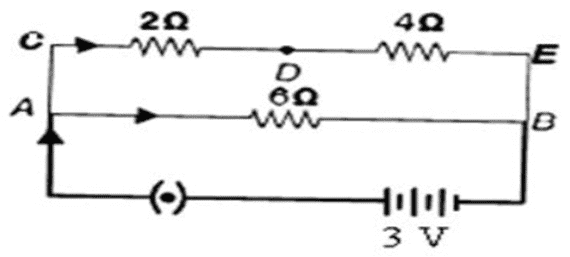
i. Total resistance in the arm CE.

ii. Total current drawn from the battery.

iii. Current in each arm, i.e., AB and CE of the circuit.

Ans. i. Total resistance in CE = R_CE = 2 + 4 = 6 Ω

ii. Total resistance of the circuit

1/R = 1/R_CE + 1/R_AB = 1/6 + 1/6 = 2/6 = 1/3

⇒ R = 3 Ω

and, V = 3 V

∴ I = ^V/_R = ³/₃ = 1 A

iii. I_AB = V/R_AB = 3/6 = 0.5 A

I_CE = V/R_CE = 3/6 = 0.5 A

Q. No. 30) Three 60 W incandescent bulbs are connected in parallel.

a. Calculate the total power consumed.

b. Now suppose that one of the bulbs is fused. What will be the total power consumed now?

Ans. a. Total power consumed = 60 x 3 = 180 W. Since wattage in parallel combination becomes three times the wattage of a single bulb.

b. Total power = 60 x 2 = 120 W.

Q. No. 31) B₁, B₂, and B₃ are three identical bulbs connected as shown in the figure below. When all three bulbs glow, a current of 3A is recorded by the ammeter A.

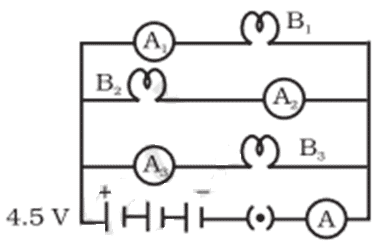
i. What happens to the glow of the other two bulbs when bulb B₁ gets fused?

ii. What happens to the reading of A₁, A₂, A₃ and A when the bulb B₂ gets fused?

iii. How much power is dissipated in the circuit when all three bulbs glow together?

Ans. i. The glow of bulbs B₂ and B₃ will remain the same.

ii. A₁ shows 1 ampere, A₂ shows zero, A₃ shows 1 ampere, and A shows 2 amperes.

iii. P = VI = 4.5 x 3 = 13.5 W

Q. No. 32) Find out the following in the electric circuit given below:

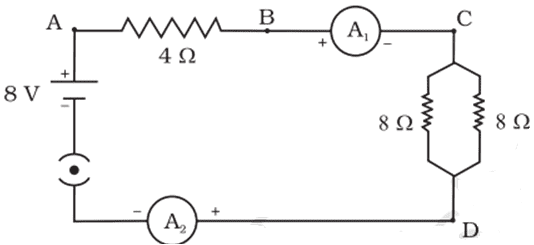
i. Effective resistance of two 8 Ω resistors in the combination.

ii. Current flowing through the 4 Ω resistor

iii. Potential difference across 4 Ω resistance

iv. Power dissipated in 4 Ω resistor

v. Difference in ammeter readings, if any.

Ans. i. ¹/_R’ = ¹/_R1 + ¹/_R2 = ¹/₈ + ¹/₈ = ²/₈ = ¹/₄

⇒ R’ = 4 Ω

ii. Total resistance of circuit R = 4 + R’ = 4 + 4 = 8 Ω

Total voltage = 8 V

∴ Total current I = ^V/_R = ⁸/₈ = 1 A

iii. V_AB = IR_AB = 1 x 4 = 4 V

iv. P_AB = I²R_AB = 1 x 1 x 4 = 4 W

v. No difference because the same current flows through each element in a series circuit.

Q. No. 33) Two lamps, one rated 100 W at 220 V and the other 200 W at 220 V are connected (i) in series and (ii) in parallel to the electric main supply of 220 V. Find the current drawn in each case.

Ans. R₁ = V²/P₁ = ^{220 x 220}/₁₀₀ = 484 Ω

R₂ = V²/P₂ = ^{220 x 220}/₂₀₀ = 242 Ω

i. In series,

R_s = R₁ + R₂ = 484 + 242 = 726 Ω

∴ I_s = V/R_s = ²²⁰/₇₂₆ = ¹⁰/₃₃ = 0.30 A

ii. In parallel,

1/R_p = 1/R₁ + 1/R₂ = 1/484 + 1/242 = 3/484

⇒ R_p = ⁴⁸⁴/₃ Ω

∴ I_p = V/R_p = ²²⁰/_484/3 = ^{220 x 3}/₄₈₄ = ³⁰/₂₂ = 1.36 A

Q. No. 34) Vinita and Ahmed demonstrated a circuit that operates the two headlights and the two sidelights of a car, in their school exhibition. Based on their demonstrated circuit, answer the following questions.

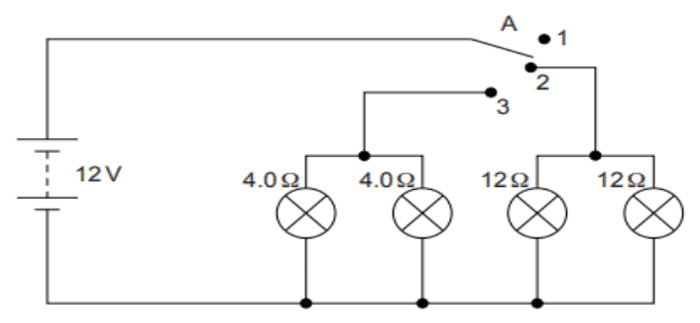
(i) State what happens when switch A is connected to

a) Position 2

b) Position 3

(ii) Find the potential difference across each lamp when lit.

(iii) Calculate the current

a. In each 12 Ω lamp when lit.

b. In each 4 Ω lamp when lit.

(iv) Show, with calculations, which type of lamp, 4.0 Ω or 12 Ω, has the higher power.

Ans. (i) a. 12 Ω lamps (only) on.

b. 4 Ω lamps (only) on.

(ii) 12 V for both sets of lamps and all of them are in parallel.

(iii) a. 12 Ω lamps are on when the wire is connected to position 2.

Voltage across both 12 Ω lamps = 12 V.

V=IR (Ohm’s law)

⇒ I = V/R

⇒ I = 12/12 = 1 A.

a. 4 Ω lamps are on when the wire is connected to position 3.

Voltage across both 4 Ω lamps = 12 V.

V=IR (Ohm’s law)

⇒ I = V/R

⇒ I = 12/4 = 3A.

(iv) P = V²/R

All lamps are in parallel and hence the same V for all lamps.

For 4 Ω lamps → P = ^12×12/₄ = 36 W

For 12 Ω lamps → P = ^12×12/₁₂ = 12 W

Hence 4 Ω lamps will have higher power.

Q. No. 35) a. Define the heating effect of current. State Joule’s law of heating.

Or,

State the law that explains the heating effect of current with respect to the measurable
properties in an electrical circuit.

b. What are the commercial unit and SI unit of electrical energy? Derive the relation between them.

c. An electric bulb with a 60 W rating operates for 10 hours and an electric fan with 100 W can run for 7 hours. Calculate the total units consumed in one day.

Ans. a. When an electric current passes through a high-resistance wire, the wire becomes hot and produces heat. This is called the heating effect of electric current.

Joule’s Law of Heating: It states that the heat produced in a resistor is:

1. Directly proportional to the square of current, H ∝ I²
2. Directly proportional to resistance for a given current, H ∝ R
3. Directly proportional to the time for which current flows through the conductor, H ∝ t

∴ H = I²Rt

b. The commercial unit is  kilowatt hour (kWh) and the SI unit is joule (J)

1 kWh = 1000 W x 60 x 60 s = 3.6 x 10⁶ Ws = 3.6 x 10⁶ J

c. We know, E = Pt

Total energy consumed in one day = 60 x 10 + 100 x 7 = 600 + 700 = 1300 Wh = 1.3 kWh = 1.3 units.

Q. No. 36) i. State a difference between the wire used in the element of an electric heater and in a fuse wire.

ii. Why is tungsten used for making filament of electrical bulbs?

iii. Why are electric bulbs filled with chemically inactive nitrogen or argon?

iv. What is meant by the statement that the rating of a fuse in a circuit is 5 A?

Ans. i. The wire used in the element of the electric heater has high resistance and high melting point whereas a fuse wire has a low resistance and low melting point.

ii. Filament of an electric bulb is made up of tungsten because:

• It does not oxidize readily at high temperatures.
• It has a high melting point.

iii. Electric bulbs are filled with chemically inactive nitrogen or argon gases to prevent oxidizing the filament due to high temperature and to prolong the life of the filament.

iv. The current in the fuse wire must not exceed 5 A otherwise it will melt and break the circuit.

Q. No. 37) i. Why are coils of electric toasters and electric irons made of an alloy rather than a pure metal?

ii. Nichrome is used to make the element of the electric heater. Why?

Ans. i. Coils of electric toasters and electric irons are made of alloys rather than pure metal because:

• The resistivity of alloys is much greater than pure metals and it changes very little with temperature.
• Alloys do not undergo oxidation (or burn) at high temperatures.

ii. Nichrome is used to make elements of electric heaters because nichrome is an alloy that has a high melting point and high resistance.

Q. No. 38) Two wires of equal length, one of copper and the other of manganin (an alloy) have the same thickness. Which one can be used for (i) Electric transmission lines and (ii) Electrical heating devices? Why?

Ans. i. Copper is used for electric transmission lines because its resistivity is low and consequently, resistance is small and power loss in transmission lines is small.

ii. Manganin alloy is used for electrical heating devices because its resistivity is high and it does not oxidize easily on heating.

Q. No. 39) The electric power consumed by a device may be calculated by either of the two expressions P = I²R or P = V²/R. The first expression indicates that it is directly proportional to R whereas the second expression indicated inverse proportionality. How can the seemingly different dependence of P on R in these expressions be explained?

Ans.

• P = I²R is used to calculate electric power when the current flowing through the circuit is constant (i.e., series combination)
• P = V²/R is used to calculate electric power when the potential difference flowing through the circuit is constant (i.e., parallel combination).

Q. No. 40) An electric kettle of 2 kW works for 2 hours daily. Calculate:

i. Energy consumed in SI and commercial unit

ii. Cost of running it in the month of June at the rate of Rs. 3 per unit.

Ans. June month is of 30 days.

i. Energy consumed in June E = Pt = 2 x 2 x 30 = 120 kWh (Commercial unit)

Again E = 120 x 3.6 X 10⁶ = 4.32 x 10⁸ J (SI unit)

ii. Required cost = Rs. 120 x 3 = Rs. 360

Q. No. 41) A torch bulb is rated 5 V and 500 mA. Calculate:

i. Its power

ii. Its resistance

iii. The energy consumed if this bulb is lighted for 4 hours.

Ans. Given, V = 5 V, I = 500 mA = 500 x 10^-3 = 0.5 A

i. Power P = VI = 5 x 0.5 = 2.5 W

ii. Resistance R = ^V/_I = ⁵/_0.5 = 10 Ω

iii. Energy consumed E = Pt = 2.5 x 4 = 10 Wh

Q. No. 42) An electric oven rated at 500 W is connected to a 220 V line and used for 2 hours daily. Calculate the cost of electric energy per month at the rate of Rs. 5 per kWh.

Ans. Energy consumed per day, E = P x t = 500 W x 2 h = 1000 Wh = 1000/1000 kWh = 1 kWh

Energy consumed in 1 month = 1 x 30 = 30 kWh

∴ Cost of electric energy = 30 x 5 = Rs. 150.

Q. No. 43) A household uses the following electrical appliances:

i. Refrigerator of rating 400 W for ten hours each day.

ii. Two electric fans of rating 80 W each for twelve hours each day.

iii. Six electric tubes of rating 18 W each for 6 hours each day.

Predict the amount of electricity bill of the household for the month of June if the cost is Rs. 3.00/unit.

Ans. June month is of 30 days.

We know, E = P x t

Electricity consumption in one day = 400 x 10 + 2 x 80 x 12 +6 x 18 x 6 = 4000 + 1920 + 648 = 6568 Wh = 6568/1000 kWh = 6.568 kWh = 6.568 units.

Electricity consumption in one month = 6.568 x 30 = 197.04 units

∴ Total cost = Rs. 197.04 x 3 = Rs. 591.12

Also Read: Chemical Reactions and Equations Class 10 Important Questions with Answers Acids, Bases, and Salts Class 10 Important Questions with Answers Metals and Non-metals Class 10 Important Questions with Answers Carbon and its Compounds Class 10 Important Questions with Answers Life Processes Class 10 Important Questions with Answers Control and Coordination Class 10 Important Questions with Answers How do Organisms Reproduce Class 10 Important Questions with Answers Heredity and Evolution Class 10 Important Questions with Answers Light Reflection and Refraction Class 10 Important Questions with Answers Human Eye and the Colourful World Class 10 Important Questions with Answers Magnetic Effects of Electric Current Class 10 Important Questions with Answers Our Environment Class 10 Important Questions with Answers

Must Also Prepare this: Electricity Class 10 Notes

Must Read: Class 10 Revision Notes Class 10 Important Questions

Hope these questions were helpful to you in preparing Class 10 Science Chapter 11 Electricity for your exams. Do share this with your friends and comment if you have any doubts/suggestions to share.